Research

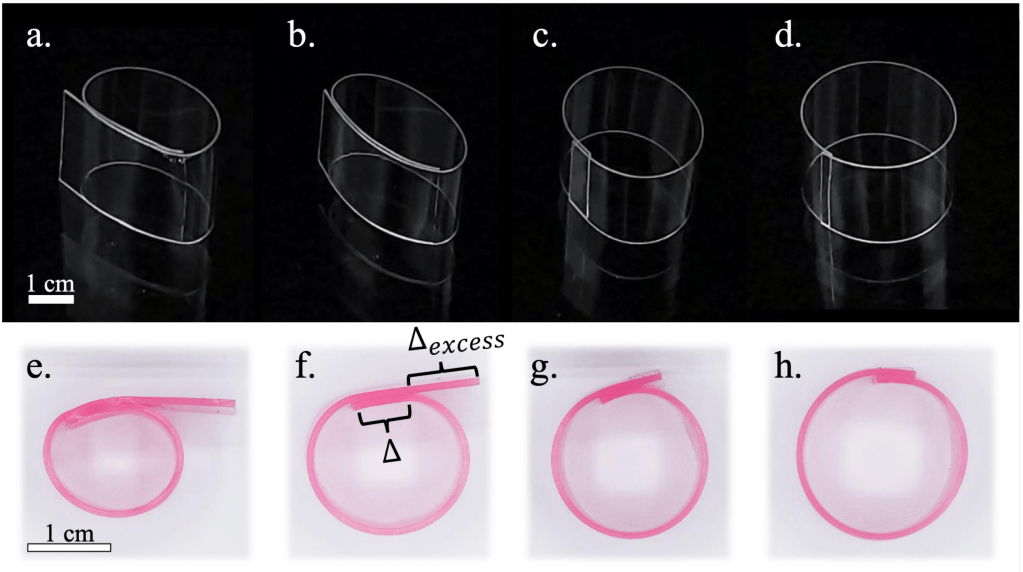
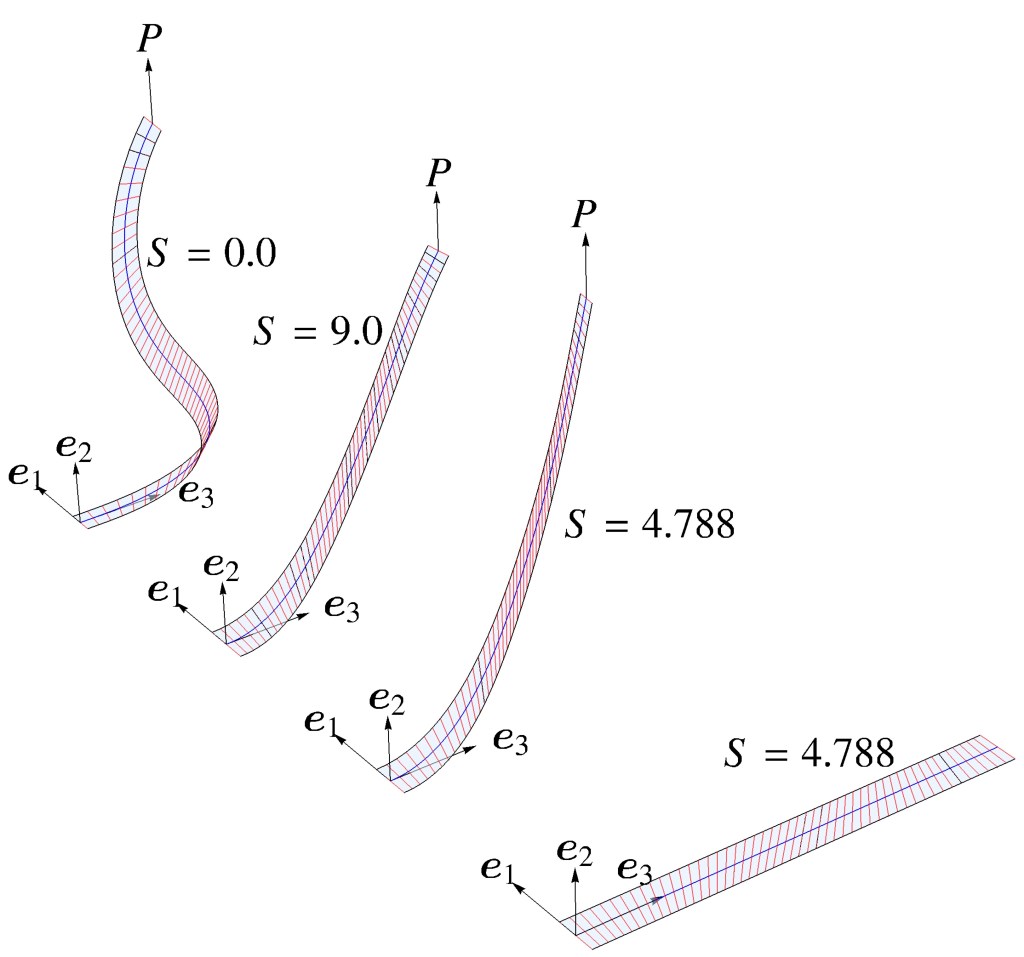
K. Suryanrayanan and H. Singh

We present a reduced order theory of locally impenetrable elastic tubes. The constraint of local impenetrability — an inequality constraint on the determinant of the 3D deformation gradient — is transferred to the Frenet curvature of the centerline of the tube via reduced kinematics. The constraint is incorporated into a variational scheme, and a complete set of governing equations, jump conditions, and boundary conditions are derived. It is shown that with the local impenetrability actively enforced, configurations of an elastic tube comprise segments of solutions of the Kirchhoff rod theory appropriately connected to segments of constant Frenet curvature. The theory is illustrated by way of three examples: a fully flexible tube hanging under self-weight, an elastic tube hanging under self-weight, and a highly twisted elastic tube.

arXiv

K. Suryanrayanan, A.B. Croll, and H. Singh

We present an experimental and theoretical study of the mechanics of an adhesive tape loop, formed by bending a straight rectangular strip with adhesive properties, and prescribing an overlap between the two ends. For a given combination of the adhesive strength and the extent of the overlap, the loop may unravel, it may stay in equilibrium, or open up quasi-statically to settle into an equilibrium with a smaller overlap. We define the state space of an adhesive tape loop with two parameters: a non-dimensional adhesion strength, and the extent of overlap normalized by the total length of the loop. We conduct experiments with adhesive tape loops fabricated out of sheets of polydimethylsiloxane (PDMS) and record their states. We rationalize the experimental observations using a simple scaling argument, followed by a detailed theoretical model based on Kirchhoff rod theory. The predictions made by the theoretical model, namely the shape of the loops the states corresponding to equilibrium, show good agreement with the experimental data. Our model may potentially be used to deduce the strength of self-adhesion in sticky soft materials by simply measuring the smallest overlap needed to maintain a tape loop in equilibrium.

arXiv

H. Singh, K. Suryanarayanan, and E.G. Virga

We study spontaneous deformations of a ribbon made of nematic polymer networks and activated under the action of a mechanical load. We show that when such ribbons are activated appropriately, the deformations produced can pull back and perform work against the externally applied load. We perform two numerical experiments to demonstrate this effect: (1) the pulling experiment, where the ribbon is pulled longitudinally by a point force, and (2) the bending experiment, where the ribbon is bent out of plane by a terminally applied point force. We quantify the capacity of the ribbon to work against external loads, and compute its dependence on both the ribbon thickness and the imprinted nematic texture (that is, the distribution of the nematic directors across the ribbon’s length). Finally, we compute the efficiency of the activation process. Building on the outcomes of our numerical explorations, we formulate two educated conjectures on how the activation efficiency can in general be improved by acting on both the applied load and the imprinted nematic texture.

arXiv and journal

H. Singh and E. G. Virga

We study the spontaneous out-of-plane bending of a planar untwisted ribbon composed of nematic polymer networks activated by a change in temperature. Our theory accounts for both stretching and bending energies, which compete to establish equilibrium. We show that when equilibrium is attained these energy components obey a complementarity relation: one is maximum where the other is minimum. Moreover, we identify a bleaching regime: for sufficiently large values of an activation parameter (which measures the mismatch between the degrees of order in polymer organization in the reference and current configurations), the ribbon’s deformation is essentially independent of its thickness.

arXiv and journal

H. Singh

We present a study on planar equilibria of a terminally loaded elastic rod wrapped around a rigid circular capstan. Both frictionless and frictional contact between the rod and the capstan are considered. We identify three cases of frictionless contact – namely where the rod touches the capstan at one point, along a continuous arc, and at two points. We show that, in contrast to a fully flexible filament, an elastic rod of finite length wrapped around a capstan does not require friction to support unequal loads at its two ends. Furthermore, we classify rod equilibria corresponding to the three aforementioned cases in a limit where the length of the rod is much larger than the radius of the capstan. In the same limit, we incorporate frictional interaction between the rod and the capstan, and compute limiting equilibria of the rod. Our solution to the frictional case fully generalizes the classic capstan problem to include the effects of finite thickness and bending elasticity of a flexible filament wrapped around a circular capstan.

supplementary video
arXiv and journal